Matriks
Video Pengerjaan
Matriks Penjumlahan, Pengurangan & Perkalian
Matriks itu kotak berisi angka yang diatur dalam baris dan kolom. ada 3 jenis operasi matriks
1.2 Penjumlahan & Pengurangan: Caranya, cukup jumlahkan atau kurangkan angka-angka yang ada di posisi yang sama.
3. Perkalian Matriks: Perlu cara khusus! Perkalian matriks mengalikan elemen baris dari matriks pertama dengan elemen kolom dari matriks kedua, lalu dijumlahkan. Hasil akhirnya adalah matriks baru.
Sumber MateriContoh Soal
1. Hitunglah hasil dari A-Z:
A = | 6 5 |
| 3 1 |
Z = | 2 4 |
| 1 2 |
Jawaban:
A - Z = | 4 1 |
| 2 -1 |
2. Hitunglah hasil M + N:
M = | 4 5 |
| 3 8 |
N = | 2 3 |
| 1 7 |
Jawaban:
M + N = | 6 8 |
| 4 14 |
3. berapakah nilai elemen di baris kedua kolom pertama dari hasil P + Q?
P = | 5 2 |
| 3 7 |
Q = | 4 1 |
| 2 6 |
Jawaban:
5
4. Hitunglah A + B - C:
A = | 6 3 |
| 4 5 |
C= | 1 2 |
B = | 2 1 | | 0 3 |
| 3 2 |
Jawaban:
A + B - C = | 7 2 |
| 7 4 |
5. Tentukan hasil dari J – K + L, dengan matriks:
J = | 5 8 |
| 6 7 |
L= | 2 1 |
K = | 1 3 | | 3 5 |
| 4 2 |
Jawaban:
J – K + L = | 6 6 |
| 5 10 |
6. Berapakah hasil dari...
| 1 -7 | | 5 -3 8 |
x
| 5 9 | | 0 2 -1 |
Jawaban:
| 1 -7 | | 5 -3 8 |
x
| 5 9 | | 0 2 -1 |
= |1x5 + (-7) x 0 1 x -3 + (-7)x 2 1x8 + (-7) x -1 |
|5x5 + 9 x 0 5 x -3 + 9 x 2 5x8 + 9 x -1 |
= |5 -17 15 |
|25 3 31 |
7. Hitunglah hasil dari P x Q:
| -3 1 | | 2 1 |
P = Q =
| 4 2 | | 5 0 |
Jawaban:
PQ=| -3 1 | x | 2 1 |
| 4 2 | x | 5 0 |
= | (-3 x 2) + (1 x 5) (-3 x 1) + (1 x 0) |
| ( 4 x 2) + (2 x 5) ( 4 x 1) + (2 x 0) |
= | -6 + 5 -3 + 0 |
| 8 + 10 4 + 0 |
= | -1 -3 |
| 18 4 |
8. Berapakah hasil dari...
| 2 -1 | | -2 0 2 |
x
| 3 0 | | 3 1 0 |
Jawaban:
| 2 -1 | | -2 0 2 |
x
| 3 0 | | 3 1 0 |
= |2 x -2 + (-1)x3 2x0 + (-1) x 1 2x2 + (-1) x 0 |
|3 x -2 + 0 x3 3x0 + 0 x 1 3x2 + 0 x 0 |
= |-4 + (-3) 0 + (-1) 4 + 0 |
|-6 + 0 0 + 0 6 + 0 |
= |-7 -1 4 |
|-6 0 6 |
9. Berapakah nilah X = Y yang memenuhi…
| x 1 | | 3 2 | | 7 4|
x =
|-1 y | | 1 0 | |-3 -2|
Jawaban:
| x 1 | | 3 2 | |3x + 1 2x|
x =
|-1 y | | 1 0 | |-3 + y -2|
|3x + 1 2x| |7 4|
=
|-3 + y -2| |-3 -2|
Sesuaikan persamaan terhadap posisi elemen, didapat:
3x + 1 = 7 -> x = 2 dan -3 -> y = 0
jadi, x + y = 2 + 0 = 2
10. Hitunglah hasil matriks perkalian dari matriks A dan B:
| 3 4 | | 7 5 |
A= B =
| 1 2 | | 6 4 |
Jawaban:
A x B = | 3 4 | | 7 5 |
x
| 1 2 | | 6 4 |
= | 3x7 + 4x6 3x5 + 4x4 |
| 1x7 + 2x6 1x5 + 2x4 |
= | 21 + 24 15 + 16 |
| 7 + 12 5 + 8 |
= | 45 31 |
| 19 13 |
11. Tentukan hasil matriks perkalian dari ordo 3 x 3 berikut:
| 1 2 3 | |9 8 7 |
A = | 4 5 6 | B= |6 5 4 |
| 7 8 9 | |3 2 1 |
Jawaban:
| 1 2 3 | |9 8 7 |
A= | 4 5 6 | B= |6 5 4 |
| 7 8 9 | |3 2 1 |
= | 1x9 + 2x6 + 3x3 1x8 + 2x5 + 3x2 1x7 + 2x4 + 3x1 |
| 4x9 + 5x6 + 6x3 4x8 + 5x5 + 6x2 4x7 + 5x4 + 6x1 |
| 7x9 + 8x6 + 9x3 7x8 + 8x5 + 9x2 7x7 + 8x4 + 9x1 |
= | 9 + 12 + 9 8 + 10 + 6 7 + 8 + 3 |
| 36 + 30 + 18 32 + 25 + 12 28 + 20 + 6 |
| 63 + 48 + 27 56 + 40 + 18 49 + 32 + 9 |
= | 30 24 18 |
| 84 69 54 |
|138 114 90 |
12. Hitunglah hasil dari...
| 1 2 | | 3 2 |
X
| 1 3 | | 4 1 |
Jawaban:
| 1 2 | | 3 2 |
X
| 1 3 | | 4 1 |
= | 1x3 + 2x4 1x2 + 2x1 |
| 1x3 + 3x4 1x2 + 3x1 |
= | 3 + 8 2 + 2 |
| 3 + 12 2 + 3 |
= | 11 4 |
| 15 5 |
Determinan Matriks
Video Pengerjaan
Determinan | Ordo 2x2 3x3 | Minor kofaktor
Well, zara mulai dari cara mencari determinan matriks terlebih dahulu. Kenapa? Soalnya, untuk mencari invers matriks, kita perlu mencari determinan matriksnya lebih dulu.
Determinan adalah nilai yang dapat dihitung dari unsur-unsur suatu matriks persegi.Determinan Matriks itu ada 2 jenis Ordo. Ordo 2x2, ordo 3x3 atau lebih
di Determinan Matriks Ordo 3x3 ada 2 cara. 1. Aturan Sarrus 2. Metode Minor Kofaktor
Sumber MateriContoh Soal
hitunglah determinan matriks ordo 2x2 dibawah:
det A = | 9 -11 |
| 0 3 |
Jawaban:
(9 x 3)-(0 x (-11)) = 27
hitunglah determinan matriks ordo 3x3: (aturan sarrus) dibawah:
Matriks A = | 4 2 8 | 4 2
| 2 1 5 | 2 1
| 3 2 4 | 3 2
Jawaban:
det A = 4.1.4 + 2.5.3 + 8.2.2 - 8.1.3 - 4.5.2 - 2.2.4
det A = 16 + 30 + 32 - 24 - 40 - 16 = -2
hitunglah determinan matriks ordo 3x3: (minor kofaktor) dibawah:
Matriks A = | 4 2 8 |
| 2 1 5 |
| 3 2 4 |
Jawaban:
det A= a11.C11 + a12.C12 + a13.C13
1.Elemen a11 (4)= 1.4 - 5.2 = 4-10 = -6
2.Elemen a12 (2)= 2.4 - 5.3 = 8-15 = -7
3.Elemen a13 (8)= 2.2 - 1.3 = 4-3 = 1
det A= a11.C11 + a12.C12 + a13.C13
= 4.(-6) + 2.(-7) + 8.1
=-24 + 14 + 8 = -2
// Tanda kofaktor ditentukan oleh (−1)i+j, di mana:
i adalah nomor baris elemen.
j adalah nomor kolom elemen.Untuk pangkat ganjil, hasilnya -1 || Untuk pangkat genap, hasilnya +1.
hitunglah determinan matriks ordo 2x2 dibawah:
A = | 2 5 |
| 4 3 |
Jawaban:
det A = | 2 5 | = (2 x 3) - (5 x 4) = 6 - 20 = -14
| 4 3 |
hitunglah determinan matriks ordo 3x3: (aturan sarrus) dibawah:
| 1 2 3 | |1 2 3 | 1 2
A = | 2 1 4 | -> det(A) = |2 1 4 | 2 1
| 3 1 2 | |3 1 2 | 3 1
Jawaban:
det(A) = 1.1.2 + 2.4.3 + 3.2.1 – 3.1.3 – 1.4.1 – 2.2.2 = 2 + 24 + 6 – 9 – 4 – 8 = 11
hitunglah determinan matriks ordo 3x3: (minor kofaktor) dibawah:
A = | 1 2 3 |
| 2 1 4 |
| 3 1 2 |
Jawaban:
det A = a11.C11 + a12.C12 + a13.C13
1. Elemen a11 (1) = (1.2) - (4.1) = 2 - 4 = -2
2. Elemen a12 (2) = (2.2) - (4.3) = 4 - 12 =-8
3. Elemen a13 (3) = (2.1) - (3.1) = 2 - 3 = -1
det A = a11 C11 + a12 C12 + a13 C13
= 1.(-2) + 2.(-8) + 3.(-1)
= -2 + 16 - 3 = 11
// Tanda kofaktor ditentukan oleh (−1)i+j, di mana:
i adalah nomor baris elemen.
j adalah nomor kolom elemen.Untuk pangkat ganjil, hasilnya -1 || Untuk pangkat genap, hasilnya +1.
hitunglah determinan matriks ordo 2x2 dibawah:
A = | 3 5 |
| 4 8 |
Jawaban:
det A = | 3 5 | = (3 x 8) - (5 x 4) = 24 - 20 = 4
| 4 8 |
hitunglah determinan matriks ordo 3x3: (aturan sarrus) dibawah:
A = | 1 2 3| 1 2
| 4 5 6| 4 5
| 7 8 9| 7 8
Jawaban:
det A = 1.5.9 + 2.6.7 + 3.4.8 - 3.5.7 - 1.6.8 - 2.4.9 = 45 + 84 + 96 - 105 - 48 - 72 = 0
hitunglah determinan matriks ordo 3x3: (Minor Kofaktor) dibawah:
A = | 1 2 3|
| 4 5 6|
| 7 8 9|
Jawaban:
det A = a11.C11 + a12.C12 + a13.C13 1. Elemen a11 (1) = (5.9) - (6.8) = 45 - 48 = -3 2. Elemen a12 (2) = (4.9) - (6.7) = 36 - 42 = -6 3. Elemen a13 (3) = (4.8) - (5.7) = 32 - 35 = -3 det A = a11.C11 + a12.C12 + a13.C13 det A = 1.(-3) + 2.(-6) + 3.(-3) = -3 + 12 + (-9) = 0 // Tanda kofaktor ditentukan oleh (−1)i+j, di mana: i adalah nomor baris elemen. j adalah nomor kolom elemen.Untuk pangkat ganjil, hasilnya -1 || Untuk pangkat genap, hasilnya +1.
hitunglah determinan matriks ordo 2x2 dibawah:
A = | -7 2 |
| 3 2 |
Jawaban:
det A = (-7).2 - 3.2 = -14 - 6 = -20
hitunglah determinan matriks ordo 3x3: (aturan sarrus) dibawah:
A = | 2 1 3 | 2 1
| 4 5 6 | 4 5
| 7 8 9 | 7 8
Jawaban:
det A = 2.5.9 + 1.6.7 + 3.4.8 = 90 + 42 + 96 = 228 3.5.7 - 2.6.8 - 1.4.9 = 105 + 96 + 36 = 237
det A = 228 - 237 = -9
hitunglah determinan matriks ordo 3x3: (minor kofaktor) dibawah:
A = | 2 1 3 |
| 4 5 6 |
| 7 8 9 |
Jawaban:
det A = a11.C11 + a12.C12 + a13.C13
1. Elemen a11 (2) = (5.9) - (6.8) = 45 - 48 = -3
2. Elemen a12 (1) = (4.9) - (6.7) = 36 - 42 = -6
3. Elemen a13 (3) = (4.8) - (5.7) = 32 - 35 = -3
det (A)= (2)(-3) - (1)(-6) + (3)(-3) = -6 + 6-9 = -9
// Tanda kofaktor ditentukan oleh (−1)i+j, di mana:
i adalah nomor baris elemen.
j adalah nomor kolom elemen.Untuk pangkat ganjil, hasilnya -1 || Untuk pangkat genap, hasilnya +1.
Eliminasi Gauss-Jordan
Materi Video
Metode Eliminasi Gauss adalah cara untuk menyelesaikan sistem persamaan linear dengan mengubah matriks menjadi bentuk yang lebih sederhana (disebut bentuk segitiga). Ciri-ciri
- 1. Jika suatu baris tidak nol semua nol, maka bilangan pertama yang tidak nol adalah 1 atau I utama (pada baris pertama, kolom pertama)
- 2. Baris nol terletak paling bawah
- 3. 1 utama berikutnya berada di kanan 1 utama baris di atasnya ( pada baris ke-2, kolom ke-2)
- 4. Di bawah 1 utama harus 0 dan dibawah 0 harus 0 0
Contoh soal
Ada suatu sistem persamaan linier, persamaannya Sbg berikut:
2x + 3y - z = 6
x + 2y - 4z = 8
x + y + 4z = 4
Pembahasan:
Pertama: ubah sistem persamaan linier menjadi matriks
| 2 3 -1 | | x | | 6 |
| 1 2 -4 | x | y | | 8 |
| 1 1 4 | | z | | 4 |
kedua: ubah Baris pertama dan kolom pertama menjadi 1
| 1 1 3 | | x | | -2 |
| 0 1 -7 | x | y | | 10 |
| 1 1 4 | | z | | 4 |
karna baris kedua depannya sudah 0 jdi lanjut ke baris ketiga ubah jd 1
| 1 1 3 | | x | | -2 |
| 0 1 -7 | x | y | | 10 |
| 0 0 1 | | z | | 6 | sudah diketahui nilai Z = 6
cari nilai Y cari nilai X
y-7z = 10 x + y + 3z = -2
y-7(6) = 10 x + 52 + 3(6) = -2
y-42 = 10 x + 52 + 18 = -2
Y = 52 x + 70 = -2 => X = -72
Ada suatu sistem persamaan linier, persamaannya Sbg berikut:
3x + y + z = 7
x - y + 2z = 4
2x + 2y - z = 3
Pembahasan:
Pertama: Hilangkan x dari (2) dan (3)
Dari (2)(x − y + 2 z = 4), substitusi x=(7 − y − z)/3 (dari Persamaan 1).
Substitusi ke (2):
7 − y − z
--------- − y + 2 z = 4
3
Kalikan semuanya dengan 3 untuk menghilangkan pecahan:
(7 − y − z) − 3y + 6z = 12
7 − 4 y + 5 z = 1 2 ⇒ − 4 y + 5 z = 5 ⇒ 4 y − 5 z = − 5 (Persamaan 4)
Substitusi ke (3):
7 − y − z
2(----------) + 2y − z = 3
3
Kalikan dengan 3:
2 (7 − y − z) + 6y − 3z = 9
14 − 2y − 2z + 6y − 3z = 9
4y − 5z = −5 (ini sama dengan Persamaan 4).
kedua: Selesaikan untuk y dan z
Dari (4), kita sudah memiliki persamaan dengan dua variabel:
4y − 5z = −5
Ambil nilai z = 3 untuk mempermudah:
4y−5(3)=−5
4y−15=−5⇒4y=10⇒y=2
ketiga: Substitusi
y=2 dan z=3 ke (1)
Dari (1):
3x+y+z=7
3x+2+3=7
3x+5=7⇒3x=2⇒x=−1
Jawaban Akhir:
x=−1,y=2,z=3
Ada suatu sistem persamaan linier, persamaannya Sbg berikut:
x + 4y + z = 11
2x + y + 3z = 14
3x + 2y + 2z = 13
Pembahasan:
Pertama: Hilangkan variabel x
Eliminasi x dari Persamaan (1), (2), dan (3).
Kali (1) dengan 2 agar x dapat dieliminasi dengan (2):
2 (x + 4y + z) = 2(11)
2x + 8y + 2z = 22 (4)
Kurangi Persamaan (4) dengan Persamaan (2):
(2x + 8y + 2z) − (2x + y + 3z) = 22 − 14
7y − z = 8 (5)
Kali (1) dengan 3 agar x dapat dieliminasi dengan (3):
3 (x + 4y + z) = 3 (11)
3x + 12y + 3z = 33 (6)
Kurangi Persamaan (6) dengan Persamaan (3):
(3x + 12y + 3z) − (3x + 2y + 2z) = 33 − 13
10y + z = 20 (7)
Kedua: Selesaikan sistem dua variabel (y dan z)
Eliminasi z dari (5) dan (7).
Kali (5) dengan 10 dan (7) dengan 7 agar nilai z setara:
10 (7y − z) = 10(8) ⇒ 70y − 10z = 80 (8)
7 (10y + z) = 7(20) ⇒ 70y + 7z = 140 (9)
Kurangi Persamaan (9) dari Persamaan (8):
(70y − 10z) − (70y + 7z) = 80 − 140
−17z = −60 ⇒ z = 60 = 3.53
17
Substitusi z ≈ 3.53 ke Persamaan (5):
7y − (3.53) = 8
7y = 8 + 3.53 ⇒ 7y = 1.53 ⇒ y ≈ 1.65
7
Ketiga: Cari nilai X
Substitusi y≈1.65 dan z≈3.53 ke Persamaan (1):
x + 4 (1.65) + (3.53) = 11
x + 6.6 + 3.53 = 11
x + 10.13 = 11 ⇒ x = 11 − 10.13 ⇒ x ≈ 0.87
Jawaban Akhir:
x ≈ 0.87, y ≈ 1.65, z ≈ 3.53
Ada suatu sistem persamaan linier, persamaannya Sbg berikut:
4x - y + z = 5
x + y + z = 8
3x - 2y + 4z = 12
Pembahasan:
Dari persamaan (2):
x + y + z = 8 ⟹ z = 8 − x − y (4)
Pertama: Substitusi z dari (4) ke (1):
4x − y + (8 − x − y) = 5
4x − y + 8 − x − y = 5
3x − 2y = −3 ⟹ y = 3x+3
2
Kedua: Substitusi z dari (4) ke (3):
3x − 2y + 4 (8 − x − y) = 12
3x − 2y + 32 − 4x − 4y = 12
−x − 6y = −20 ⟹ x + 6y = 20 (6)
Ketiga: Substitusi y dari (5) ke (6):
(3x + 3)
x + 6 ------ = 20
2
x + 9x + 9 = 20
10x = 11 ⟹ x = 1.1
Kempat: Substitusi x = 1.1 ke (5):
3(1.1) + 3 6.3
y = ---------- = --- = 3.15
2 2
Substitusi x dan y ke (4):
z = 8 − x − y = 8 − 1.1 − 3.15 = 3.75
Hasil Akhir:
x = 1.1, y = 3.15, z = 3.75
Ada suatu sistem persamaan linier, persamaannya Sbg berikut:
5x + 2y + z = 10
x + 4y - z = 5
3x + y + 2z = 8
Jawaban:
Dari persamaan (2):
x + 4y − z = 5 ⟹ z = x + 4y − 5 (4)
Pertama: Substitusi z dari (4) ke (1):
5x + 2y + (x + 4y − 5) = 10
6x + 6y = 15 ⟹ x + y = 2.5 (5)
Kedua: Substitusi z dari (4) ke (3):
3x + y + 2 (x + 4y − 5) = 8
3x + y + 2x + 8y − 10 = 8
5x + 9y = 18 (6)
Dari (5) dan (6):
Ketiga: Substitusi y = 2.5 − x dari (5) ke (6):
5 x + 9 (2.5 − x) = 18
5x + 22.5 − 9x = 18
−4x = −4.5 ⟹ x = 1.125
Keempat: Substitusi x = 1.125 ke (5):
1.125 + y = 2.5 ⟹ y = 1.375
Substitusi x dan y ke (4):
z = x + 4y − 5 = 1.125 + 4 (1.375) − 5 = 1.625
Hasil Akhir:
x = 1.125, y = 1.375, z = 1.625
Ada suatu sistem persamaan linier, persamaannya Sbg berikut:
2x + 4y - 3z = 6
3x + y + z = 7
x + 2y + 4z = 8
Pembahasan:
Representasikan dalam bentuk matriks:
| 2 4 -3 | | x | | 6 |
| 3 1 1 | x | y | | 7 |
| 1 2 4 | | z | | 8 |
Buat elemen pertama baris pertama (pivot) menjadi 1 dengan membagi baris pertama oleh 2:
| 1 2 -1.5 | | x | | 3 |
| 3 1 1 | x | y | | 7 |
| 1 2 4 | | z | | 8 |
Eliminasi elemen di bawah pivot:
Baris 2: Baris 2−3×Baris 1Baris 3: Baris 3−Baris 1
Hasil:
| 1 2 -1.5 | | x | | 3 |
| 0 -5 5.5 | x | y | | -2 |
| 0 0 5.5 | | z | | 5 |
Ubah pivot berikutnya menjadi 1:
Baris 2: Baris 2 ÷ −5 Baris 3: Baris 3 ÷ 5.5
Hasil:
| 1 2 -1.5 | | x | | 3 |
| 0 1 -1.1 | x | y | | 0.4 |
| 0 0 1 | | z | | 0.91 |
Dari Baris 3: z = 0.91 Dari Baris 2: y − 1.1 z = 0.4 ⟹ y = 0.4 + 1.1 (0.91) = 1.41 Dari Baris 1: x + 2y − 1.5z = 3 ⟹ x = 3 − 2 (1.41) + 1.5 (0.91) = 0.84
Jawaban:
x = 0.84, y = 1.41, z = 0.91
Ada suatu sistem persamaan linier, persamaannya Sbg berikut:
x + 5y + z = 9
4x + 2y - z = 5
2x + 3y + z = 7
Pembahasan:
Representasikan dalam bentuk matriks:
| 1 5 1 | | x | | 9 |
| 4 2 -1 | x | y | | 5 |
| 2 3 1 | | z | | 7 |
Pertama: Buat elemen pertama baris pertama menjadi 1 (sudah dilakukan). Eliminasi elemen di bawah pivot:
Baris 2: Baris 2 − 4 × Baris 1Baris 3: Baris 3 − 2 × Baris 1
Hasil:
| 1 5 1| | x | | 9 |
| 0 -18 -5| x | y | |-31|
| 0 -7 -1| | z | |-11|
Kedua: Ubah pivot kedua menjadi 1 dengan membagi baris kedua oleh -18:
Baris 2: Baris 2 ÷ −18
Hasil:
| 1 5 1| | x | | 9 |
| 0 1 0.28| x | y | |1.72|
| 0 -7 -1| | z | |-11|
Ketiga: Eliminasi elemen di bawah pivot:
Baris 3: Baris 3 + 7 × Baris 2
Hasil:
| 1 5 1| | x | | 9 |
| 0 1 0.28| x | y | |1.72|
| 0 0 1| | z | |1.04|
Dari Baris 3: z = 1.04 Dari Baris 2: y + 0.28 z = 1.72 ⟹ y = 1.72 − 0.28 (1.04) = 1.43 Dari Baris 1: x + 5y + z = 9 ⟹ x = 9 − 5 (1.43) − 1.04 = 1.81
Jawaban:
x = 1.81, y = 1.43, z = 1.04
Ada suatu sistem persamaan linier, persamaannya Sbg berikut:
x - y + z = 3
2x + y - z = 5
x + 2y + 3z = 12
Pembahasan:
Representasikan dalam bentuk matriks:
| 1 -1 1 | | x | | 3 |
| 2 1 -1 | x | y | | 5 |
| 1 2 3 | | z | | 12 |
Pertama: Eliminasi elemen di bawah pivot:
Baris 2: Baris 2 − 2 × Baris 1 Baris 3: Baris 3 − Baris 1
Hasil:
| 1 -1 1 | | x | | 3 |
| 0 3 -3 | x | y | | -1|
| 0 3 2 | | z | | 9 |
Kedua: Eliminasi elemen di bawah pivot:
Baris 3: Baris 3−Baris 2
Hasil:
|1 -1 1 | | x | | 3 |
|0 3 -3 | x | y | |-1 |
|0 0 5 | | z | |10 |
Dari Baris 3: z = 10/5 = 2 Dari Baris 2: 3y − 3z = −1 ⟹ y = (−1 + 3(2))/3 = 1 Dari Baris 1: x − y + z = 3 ⟹ x = 3 + 1 −2 = 2
Jawaban:
x = 2, y = 1, z = 2
Ada suatu sistem persamaan linier, persamaannya Sbg berikut:s
x + 2y - z = 6
2x - y + 3z = 14
3x + y + z = 10
Pembahasan:
Representasi dalam Matriks:
|1 2 -1 | | x | | 6 |
|2 -1 3 | | y | | 14|
|3 1 1 | | z | | 10|
Langkah Penyelesaian:
Pertama: Eliminasi elemen di bawah pivot:
Baris 2: Baris 2 − 2 × Baris 1, Baris 3: Baris 3 − 3 × Baris 1
Hasil:
|1 2 -1 | | x | | 6 |
|0 -5 5 | | y | | 2 |
|0 -5 4 | | z | |-8 |
Eliminasi elemen di bawah pivot:
Baris 3: Baris 3 − Baris 2
Hasil:
|1 2 -1 | | x | | 6 |
|0 -5 5 | | y | | 2 |
|0 0 -1 | | z | |-10|
-10 2 - 5(10)
z= --- = 10, y = --------- = 10, x = 6 - 2(10) + 10 = -4
-1 -5
Jawaban:
X = −4, Y = 10, Z = 10
Ada suatu sistem persamaan linier, persamaannya Sbg berikut:
2x - 3y + z = 1
x + y - 4z = -2
3x - y - 2z = 8
Pembahasan:
Representasi dalam Matriks:
|2 -3 1 | | x | | 1 |
|1 1 -4 | | y | | -2|
|3 -1 -2 | | z | | 8|
Pertama: Eliminasi elemen di bawah pivot:
Baris 2: Baris 2 − 0.5 × Baris 1, Baris 3: Baris 3 − 1.5 × Baris 1Hasil:
|2 -3 1 | | x | | 1 |
|0 2.5 -4.5| | y | |-2.5|
|0 3.5 0.5| | z | | 6.5|
Kedua: Eliminasi elemen di bawah pivot kedua:
(3.5 )
Baris 3: Baris 3−(--- x Baris 2)
(2.5 )
Hasil:
|2 -3 1 | | x | | 1 |
|0 2.5 -4.5| | y | |-2.5|
|0 0 7.8| | Z | |10.1|
10.1
z = ---- = 1.29
7.8
-2.5-(-4.5 x 1.29) -2.5 + 5.805 3.305
y = ----------------- = ----------- = ----- = 1.32
2.5 2.5 2.5
1 − (−3 × 1.32) + (1.29) 1 + 3.96 + 1.29 6.25
x = ------------------------ = --------------- = ---- = 3.12
2 2 2
Jawaban Akhir:
x ≈ 3.12, y ≈ 1.32, z ≈ 1.29
Ada suatu sistem persamaan linier, persamaannya Sbg berikut:s
x + 2y + z = 7
3x - y + 4z = 10
2x + 3y - z = 5
Pembahasan:
Representasi matriks
|1 2 1 | | x | | 7 |
|3 -1 4 | | y | |10 |
|2 3 -1 | | z | |5 |
Pertama: Eliminasi elemen di bawah pivot pertama:
Baris 2: Baris 2 − 3 × Baris 1, Baris 3: Baris 3 − 2 × Baris 1
Hasil:
| 1 2 1 | | x | | 7 |
| 0 -7 1 | | y | |-11|
| 0 -1 -3 | | z | |-9 |
Kedua: Eliminasi elemen di bawah pivot kedua:
-1
Baris 3: Baris 3 --- x Baris 2
−7
Hasil:
| 1 2 1 | | x | | 7 |
| 0 -7 1 | | y | |-11|
|0 0 -3.142| | z | |-10.57|
-10.57
z = ------ = 3.36
-3.142
-11 -(1 x 3.36) -11 - 3.36
y = --------------- = --------- = 2.05
-7 -7
x = 7 − (2 × 2.05) − 3.36 ≈ 7 − 4.1 − 3.36 ≈ -0.46
x ≈ −0.46, y ≈ 2.05, z ≈ 3.36
Ada suatu sistem persamaan linier, persamaannya Sbg berikut:
4x - 3y + z = 2
x + y - 2z = 6
2x - y + 3z = 5
Pembahasan:
Representasi matriks
| 4 -3 1 | | x | | 2 |
| 1 1 -2 | | y | | 6 |
| 2 -1 3 | | z | | 5 |
Pertama: Eliminasi elemen di bawah pivot pertama:
1 2
Baris 2: Baris 2 - - x Baris 1, Baris 3: Baris 3 - - x Baris 1
4 4
| 4 -3 1 | | x | | 2 |
|0 2.25 -2.25| | y | |5.5|
|0 0.5 2.5 | | z | | 3 |
Kedua: Eliminasi elemen di bawah pivot kedua:
Baris 3: Baris 3
0.5
Baris 3: Baris 3− ---- x Baris 2
2.25
Hasil:
| 4 -3 1 | | x | | 2 |
|0 2.25 -2.25| | y | |5.5|
|0 0 2.883| | z | |4.223|
4.223
z = ----- = 1.46
2.883
5.5 - (-2.25) × 1.46)
y = --------------------- = 3.0
2.25
2 + 3(3.0) - (1.46)
x = ------------------ = 2.64
4
x ≈ 2.64, y ≈ 3.0, z ≈ 1.46
Invers Matriks
Materi Video
Invers matriks itu gampangnya adalah "kebalikan" dari suatu matriks. Kalau kamu punya matriks A, terus dikalikan sama invers-nya (A−1), hasilnya bakal jadi matriks identitas I (matriks yang ada angka 1 di diagonal utamanya dan 0 di sisanya).
Cara Hitung Invers Matriks- 1. Hitung determinannya dulu. Ini kayak nilai "pengaruh" dari matriks itu. Kalau determinannya 0, nggak ada inversnya alias matriksnya singular.
- 2. Gunakan determinan buat hitung kofaktor. Di matriks 2x2, ini lebih simpel karena udah ada rumus cepatnya: tukar elemen diagonal utama, lalu ubah tanda elemen diagonal kedua.
- 3. Bagi setiap elemen dengan determinan. Nah, ini dia yang bikin jadi invers.
Contoh Soal
1. Tentukan invers dari:
A-1 = |1 0|
|0 1|
Jawaban:
A-1= |1 0|
|0 1| (karena matriks identitas)
2. Tentukan invers dari:
B= |7 -5|
|3 -2|
Jawaban:
|B| = (7 x -2) - (3 x -5) = -14 + 15 = 1
B-1 = | -2 5|
|-3 7|
3. Tentukan invers dari:
C = | -1 2 |
| 3 -4 |
Jawaban:
|C| = ( -1 x -4 - 3 x 2 ) = 4 - 6 = -2
C-1 = 1| -4 -2 |
-2| -3 -1 |
4. Tentukan invers dari:
D = |2 -1|
|-3 5|
Jawaban:
|D| = (2 x 5) - (-3 x -1) = 10 - 3 = 7
D-1 = 1 |5 1|
7 |3 2|
5. carilah E-1
E = | 1 2 |
| 3 4 |
Jawaban:
|E| = (1 x 4) - (3 x 2) = 4 - 6 = -2
E-1 = | 4 -2| = | -2 1|
|-3 1| |1.5 -0.5|
6. Hitung invers dari:
F = | 5 3 |
| 2 1 |
Jawaban:
|F| = (5 x 1) - (2 x 3) = 5 - 6 = -1
F-1 = 1 | 1 -3| = | -1 3|
|-2 5| | 2 -5|
7. Hitung invers dari:
G = | 3 -2 |
| -1 4 |
Jawaban:
|G| = (3 x 4) - (1 x -2) = 12 - 2 = 10
G-1 = 1| 4 2|
10| 1 3|
8. Hitung invers dari:
H = | 2 5 |
| 7 8 |
Jawaban:
H = (2 x 8) - (7 x 5) = 16 - 35 = -19
H-1 = | -8 5|
|7 -2|
9. Carilah invers Matriks
I = | 4 7 |
| 2 6 |
Jawaban:
|I| = (4 x 6) - (2 x 7) = 24 - 14 = 10
I-1 = 1 | 6 -7|
10 |-2 4|
10. Hitung invers dari:
J = | 1 1 |
| 3 2 |
Jawaban:
J = (1 x 2) - (3 x 1) = 2 - 3 = -1
J-1 = 1| 2 -1| = | -2 1|
-1|-3 1| | 3 -1|
11. Tentukan apakah matriks ini memiliki Invers?
K = | 1 2 |
| 2 4 |
Jawaban:
|K| = (1 x 4) - (2 x 2) = 4 - 4 = 0
Karena B = 0, maka matriks ini tidak memiliki invers.
12. Hitung invers dari:
L = | 2 3 |
| 1 4 |
Jawaban:
L = (2 x 4) - (1 x 3) = 8 - 3 = 5
L-1 = 1 | 4 -3|
5 |1 2|
Komputer Grafik
Materi Video
Dalam komputer grafik, matriks digunakan untuk transformasi gambar, seperti:
- Translasi : Memindahkan posisi gambar ke tempat lain. Sumber Materi
- Scaling : Mengubah ukuran gambar, bisa diperbesar atau diperkecil. Sumber Materi
- Reflection: Membalik gambar terhadap suatu sumbu. Sumber Materi
- Rotation : Memutar gambar dengan sudut tertentu. Sumber Materi
Contoh Soal(Translasi, Scalling, Reflection, Rotation)
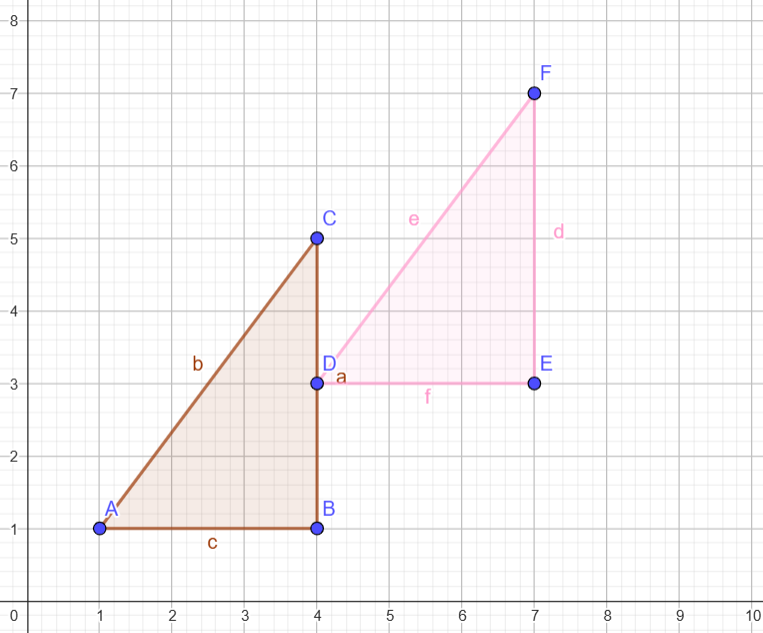
Contoh 1 Translasi (geser kanan/kiri)
Geser ke kanan dan ke atas:
Koordinat Awal: A(1, 1), B(4, 1), C(4, 5)
Translasi: Geser titik sejauh tx= 3 ke kanan dan ty= ke atas.
Hasil Titik: D'(4, 3), E'(7, 3), F'(7, 7).
Contoh 1 Scaling (pengecilan/pembesaran)

Pembesaran seragam:
Koordinat Awal: A(1, 2), B(3, 2), C(3, 5)
Scaling:Faktor s x= 2, sy= 2
Hasil Titik: D'(2, 4), E'(6, 4), F'(6, 10).
Contoh 1 Refleksi
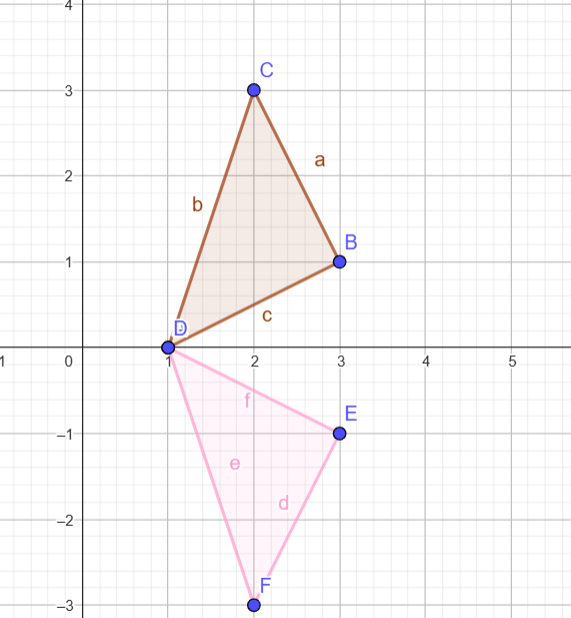
Refleksi terhadap sumbu X:
Koordinat Awal: A(1, 0), B(3, 1), C(2, 3)
Reflection: Cerminkan terhadap sumbu x.
Hasil Titik: D'(1, 0), E'(3, -1), F'(2, -3).
Contoh 1 Rotasi
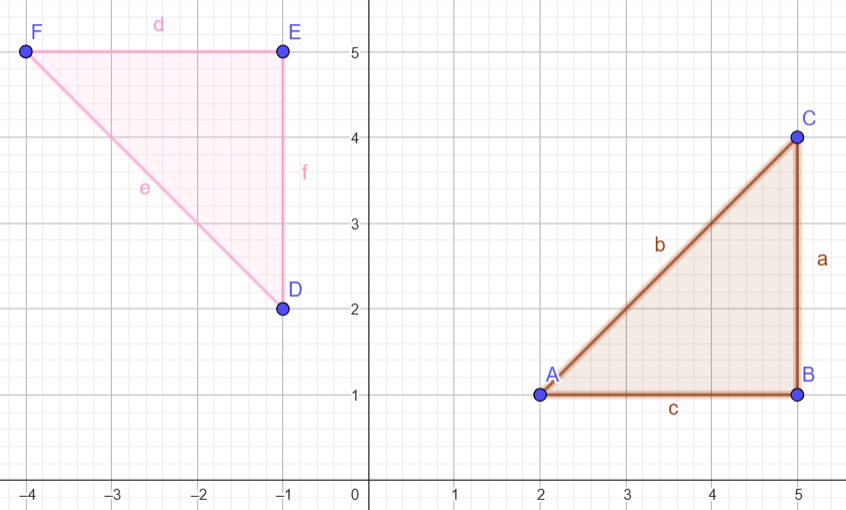
Rotasi 90∘ berlawanan arah jarum jam:
Koordinat Awal: A(2, 1), B(5, 1), C(5, 4)
Rotation: Putar sebesar 90∘ berlawanan arah jarum jam dengan pusat (0, 0).
Hasil Titik: D'(-1, 2), E'(-1, 5), F'(-4, 5).
Contoh 2 Translasi (geser kanan/kiri)
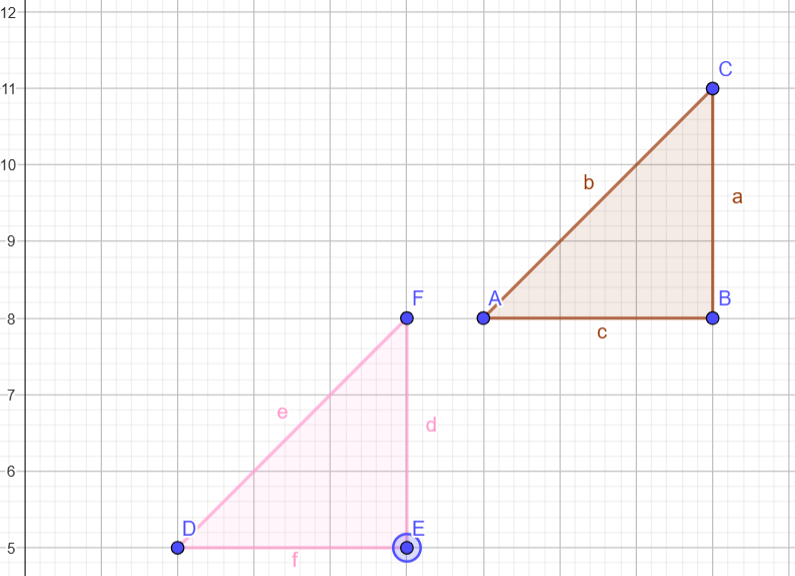
Geser ke kiri dan ke bawah:
Koordinat Awal: A(6, 8), B(9, 8), C(9, 11)
Translasi: Geser titik sejauh tx = −4 ke kiri dan t y = 3 ke bawah.
Hasil Titik: D'(2, 5), E'(5, 5), F'(5, 8).
Contoh 2 Scaling (pengecilan/pembesaran)
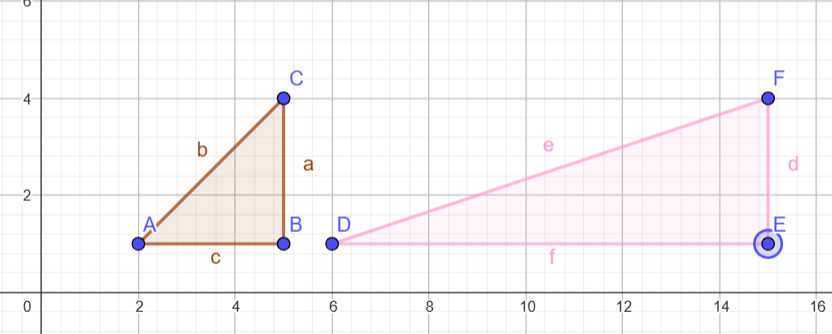
Pembesaran pada X:
Koordinat Awal: A(2, 1), B(5, 1), C(5, 4)
Scaling:Faktor s x= 3, sy= 1
Hasil Titik: D'(6, 1), E'(15, 1), F'(15, 4).
Contoh 2 Refleksi
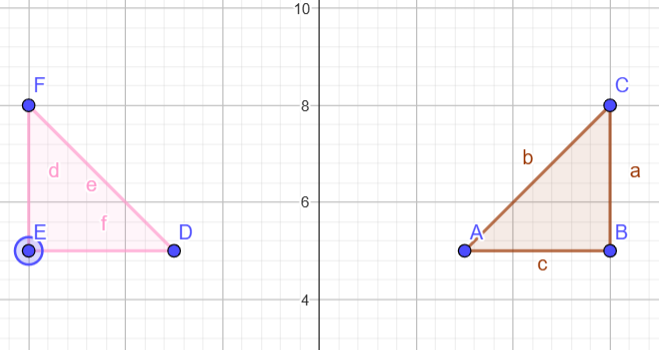
Refleksi terhadap sumbu y:
Koordinat Awal: A(3, 5), B(6, 5), C(6, 8)
Reflection: Cerminkan terhadap sumbu y
Hasil Titik: D'(-3, 5), E'(-6, 5), F'(-6, 8).
Contoh 2 Rotasi
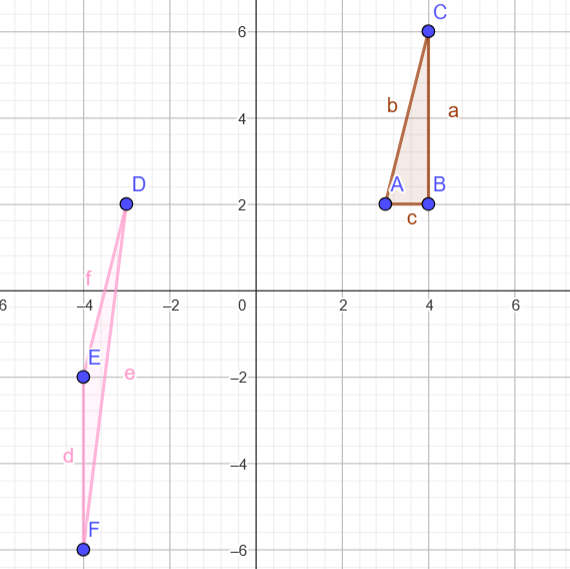
ROTASI 180∘:
Koordinat Awal: A(3, 2), B(4, 2), C(4, 6) Rotation: Putar sebesar 180∘ dengan pusat (0, 0). Hasil Titik: D'(-3, -2), E'(-4, -2), F'(-4, -6).Contoh 3 Translasi (geser atas/bawah)
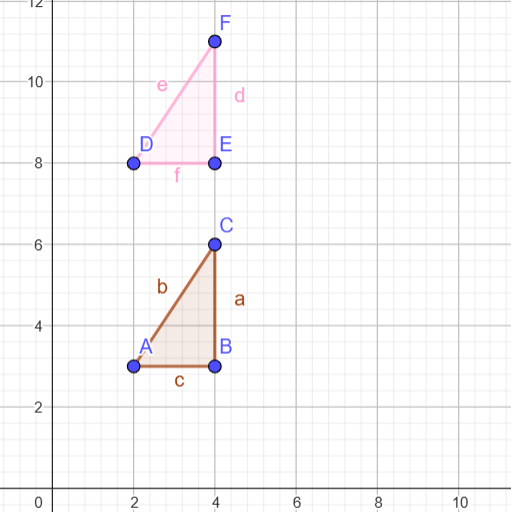
Translasi di sumbu y saja:
Koordinat Awal: A(2, 3), B(4, 3), C(4, 6)
Translasi: Geser titik sejauh t2= 0 ty= 5 ke atas
Hasil Titik: D'(2, 8), E'(4, 8), F'(4, 11).
Contoh 3 Scaling (pengecilan/pembesaran)
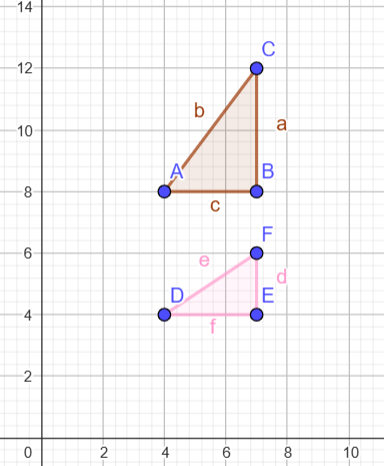
Pengecilan hanya pada y:
Koordinat Awal: A(4, 8), B(7, 8), C(7, 12)
Scaling: Faktor sx = 1 dan sy = 0,5
Hasil Titik: D'(4, 4), E'(7, 4), F'(7, 6).
Contoh 3 Refleksi
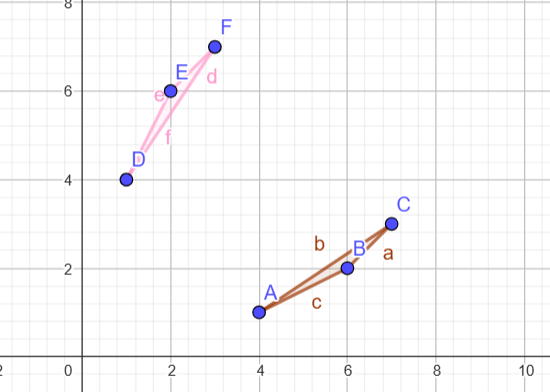
Refleksi terhadap garis y = x:
Koordinat Awal: A(4, 1), B(6, 2), C(7, 3)
Reflection: Cerminkan terhadap garis y=x.
Hasil Titik: D'(1, 4), E'(2, 6), F'(3, 7).
Contoh 3 Rotasi
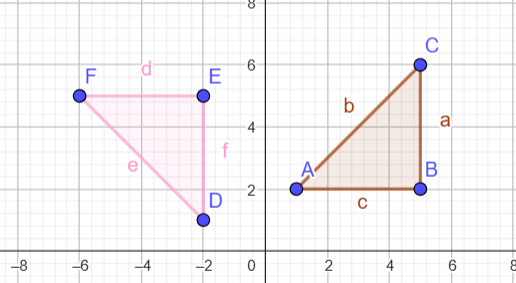
Rotasi 270∘ searah jarum jam:
Koordinat Awal: A(1, 2), B(5, 2), C(5, 6)
Rotation: Putar sebesar 270∘ searah jarum jam dengan pusat (0, 0).
Hasil Titik: D'(-2, 1), E'(-2, 5), F'(-6, 5).
Kriptografi
Materi Video
Kriptografi adalah ilmu untuk menyandikan pesan agar lebih aman. Berikut istilah-istilah yang sering digunakan:
- Plaintext (P): Isi pesan asli yang ingin dikirim.
- Ciphertext (C): Hasil enkripsi dari plaintext, berupa teks yang tidak bisa langsung dimengerti.
- Enkripsi (fungsi E): Proses mengubah plaintext menjadi ciphertext.
- Dekripsi (fungsi D): Proses mengembalikan ciphertext menjadi plaintext asli.
- Kunci: Bilangan rahasia yang dipakai untuk enkripsi dan dekripsi.
- zara punya pesan 𝑃, lalu lakukan enkripsi E(P) menggunakan kunci, hasilnya C.
A|B|C|D|E|F|G|H|I|J|K |L |M |N |O |P |Q |R |S |T |U |V |W |X |Y |Z matriks kunci = | 2 1 | //bekas contoh MK di 0|1|2|3|4|5|6|7|8|9|10|11|12|13|14|15|16|17|18|19|20|21|22|23|24|25 | 3 4 | tulis kelas
Contoh Kalimat yg Terenkripsi dan Terdekripsi
HALO > "OUKL"
H=7, A=0 L=11, O=14
| 2 1 | |7|(2x7)+(1x0) |14| mod 26 = 14 O | 2 1 | |11|(2x11)+(1x14) |36| mod 26 = 10 K
x = -- x = --
| 3 4 | |0|(3x7)+(4x0) |21| mod 26 = 21 U | 3 4 | |14|(3x11)+(4x14) |89| mod 26 = 11 L
Verifikasi dengan Deskripsi:
Matriks kunci = | 2 1 | det: 2 x 4 - 1 x 3 = 8 - 3 = 5
| 3 4 | Invers determinan 5 mod 26 = 21 (karena 5 ⋅ 21 ≡ 1 mod 26).
Invers M k = 1. | 4 -1 | mod 26 = | 4 25 |
det |-3 2 | | 23 2 |
gunakan hasil Ciphertext (KL)
|4 25 | |10| | 4x10 + 25x11 | | 40 + 275 | | 315 mod 26 = 7 H |
x = = =
|23 2 | |11| | 23x10 + 2x11 | | 230 + 22 | | 252 mod 26 = 0 A |
gunakan hasil Ciphertext (OU)
|23 2 | |21| | 23x14 + 2x21 | | 322 + 42 | | 364 mod 26 = 11 L |
x = = =
| 4 25 | |14| | 4x14 + 25x21 | | 56 + 525 | | 581 mod 26 = 14 O |
BU > "WF"
B=1, U=20
| 2 1 | |1|(2x1)+(1x20) |22| mod 26 = 22 W
x = --
| 3 4 | |20|(3x1)+(4x20) |83| mod 26 = 5 F
Verifikasi dengan Deskripsi:
matriks kunci = | 2 1 | det: 2 x 4 - 1 x 3 = 8 - 3 = 5
| 3 4 | Invers determinan 5 mod 26 = 21
Invers M k = 1. | 4 -1 | mod 26 = | 4 25 |
det |-3 2 | | 23 2 |
gunakan hasil Ciphertext (WF)
|23 2 | |22| | 23x5 + 2x6 | | 115 + 12 | | 127 mod 26 = 1 B |
x = = =
|4 25 | |5| | 4x5 + 25x6 | | 20 + 150 | | 170 mod 26 = 20 U |
Yulis > "QUERCG"
Y=24 U=20 L=11, I=8, S=18 X=1
| 2 1 | |24| (2x24)+(1x20) 68 mod 26 = 16 Q | 2 1 | |11| (2x11)+(1x8) 30 mod 26 = 4 E | 2 1 | |18| (2x18)+(1x18) 54 mod 26 = 2 C
x = = -- x = = --
| 3 4 | |20| (3x24)+(4x20) 152 mod 26 = 20 U | 3 4 | |8| (3x11)+(4x8) 43 mod 26 = 17 R | 3 4 | |1| (3x18)+(4x1) 58 mod 26 = 6 G
Verifikasi dengan Deskripsi:
matriks kunci = | 2 1 | det: 2 x 4 - 1 x 3 = 8 - 3 = 5
| 3 4 | Invers determinan 5 mod 26 = 21
Invers M k = 1. | 4 -1 | mod 26 = | 4 25 |
det |-3 2 | | 23 2 |
gunakan hasil Ciphertext (QUERCG)
|23 2 | |16| | 23x16 + 2x24 | | 368 + 48 | | 416 mod 26 = 24 Y |
x = = =
|4 25 | |20| | 4x20 + 25x20 | | 80 + 500 | | 580 mod 26 = 20 U |
x = = =
|23 2 | |4 | | 23x4 + 2x11 | | 92 + 22 | | 114 mod 26 = 11 L |
x = = =
|4 25 | |17| | 4x17 + 25x8 | | 68 + 200 | | 268 mod 26 = 8 I |
x = = =
|23 2 | |2 | | 23x2 + 2x18 | | 46 + 36 | | 82 mod 26 = 18 S |